Jacobi iterations and vector rotation

The Jacobi method [see wiki] for solving liner system is based on the fact that matrix multiplication will rotate the vector and converge if the infinity norm of Eigen values are less than 1.

From a practical point of view, the performance of convergence is determined by the spectral radius [see wiki] of the matrix. and the small the spectral radius the better.

CORDIC computations are also a sequence of rotations but the rotation matrix is adaptive. the spectral radius of rotation matrix is always 1, but when rotating using shift & add, the spectral radius is slightly bigger than 1, but as the rotation angle –>0, the spectral radius->1, so resulting vector converge to the set angle/point. more information about CORDIC please check these papers.

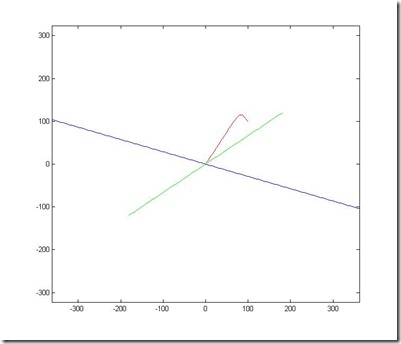
I have also wrote a matlab script for visualizing the path of the vector converge/ diverge. the red curve shows the path, and green/blue lines are the lines defined by eigenvectors. note that the rotation vector is random.

%%  eig value roatation divergence/ convegence
N=100; %number of interations
r=rand(2,2);

[l v]=eig(r);
x=N*ones(1:N,2);
eigenvalu_max=max(max(v))
if eigenvalu_max<1.1 

    for i=1:N+1
        x(i+1,:)=r*x(i,:)';
    end
end

%compass(x(:,1),x(:,2));
plot(x(:,1),x(:,2),'r'); axis equal; hold on
plot([-N:N]'./l(1,1),[-N:N]'./l(2,1),'g');
plot([-N:N]'./l(1,2),[-N:N]'./l(2,2),'b'); hold off;

the path of convergence some oscillate along the way down to 0, this another interesting fact about eigenvalues, so far I am still not very sure the exact reason, but I have some ideas, maybe I will post another one when I got the time to prove it.